Stokes' Law

George Gabriel Stokes derived the expression, in 1851, for the frictional force exerted on spherical objects with very small Reynolds numbers (e.g., very small particles) in a continuous viscous fluid by solving the small fluid-mass limit of the generally unsolvable Navier-Stokes equations:

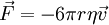
where:

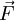is the frictional force

r is the Stokes radius of the particle

η is the fluid viscosity, and

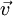is the particle's speed

where:

If the particles are falling in the viscous fluid by their own weight, then a terminal velocity, also known as the settling velocity, is reached when this frictional force combined with the bouyant force exactly balance the gravitational force. The resulting settling velocity is given by

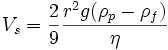
where:

V_s is the particles' settling velocity
      (vertically downwards if ρ_p > ρ_f, upwards if ρ_p < ρ_f)
   g is the acceleration due to gravity;
   ρ_p is the density of the particles;
   ρ_f is the density of the fluid

 

Also see Stokes Theorem.