in differential geometry is a statement about the
integration of differential forms which generalizes several theorems from
vector calculus. Let M be an oriented piecewise smooth manifold
of dimension n and let ω be an n−1
form that is a "compactly supported" "differential form" on M of
class C. If ∂M denotes the boundary of M with its induced
orientation, then:
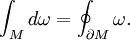
Here d is the "exterior derivative", which is defined using the
manifold structure only. The Stokes theorem can be considered as a
generalization of the fundamental theorem of calculus. The theorem is
often used in situations where M is an embedded oriented submanifold of
some bigger manifold on which the form ω is
defined.
Application
Notes:
