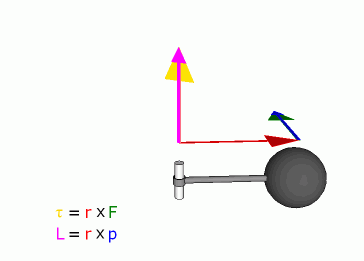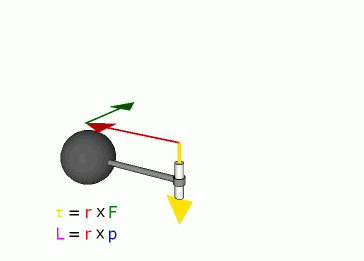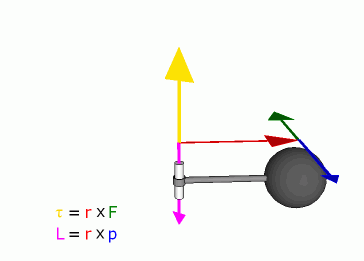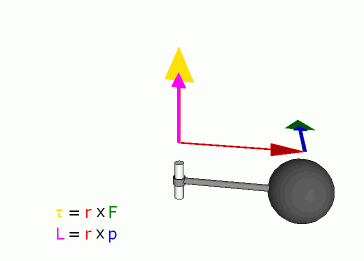angular momentum

---

of an object rotating about some reference point is the measure of the extent to which the object will continue to rotate about that point unless acted upon by an external torque.

In particular, if a point mass rotates about an axis, then the angular momentum with respect to a point on the axis is related to the mass of the object, the velocity and the distance of the mass to the axis.

Definition

Angular momentum of a particle about some origin is defined as:

where:

is the angular momentum of the particle,

is the position of the particle expressed as a displacement vector from the origin,

is the linear momentum of the particle, and

is the vector cross product.

The angular momentum are newton-meter-seconds; N·m·s (kgm²s^-1).

Because of the cross product, L is a pseudovector perpendicular to both the radial vector r and the momentum vector p.

If a system consists of several particles, the total angular momentum about an origin can be obtained by adding (or integrating) all the angular momenta of the constituent particles. Angular momentum can also be calculated by multiplying the square of the displacement r, the mass of the particle and the angular velocity.